일렬로 늘어선 같은 종류의 자료 여러 개를 저장하기 위한 가장 기초적인 자료 구조는 '배열(array)'이다. 이 포스팅에서는 배열과 같이 일렬로 늘어선 자료들을 저장하기 위한 자료 구조인 '동적 배열'과 '연결 리스트'에 대해 다룬다. 이 둘은 배열과 비슷하지만, 배열에서는 비효율적이거나 할 수 없는 작업들을 효율적으로 할 수 있도록 도와준다. 두 자료 구조는 서로 다른 특성을 갖고 있으며, 이 책에 나오는 다른 자료 구조들을 구현하기 위해서도 사용되는 중요한 재료이다.
동적 배열
배열의 문제점은 처음 배열을 선언할 때 배열의 크기를 지정해야 하며, 그 이상의 자료를 집어넣을 수 없다는 점이다. 이 문제를 해결하기 위해 고안된 것이 자료의 개수가 변함에 따라 크기가 변경되는 동적 배열(Dynamic Array)이다. 이는 언어 차원에서 지원되는 것이 아니라 배열을 이용해서 만들어 낸 별도의 자료구조이다. 때문에 보통 언어의 표준 라이브러리에 포함되어 있다. (자바에서는 ArrayList를 통해 사용 가능하다)
- 특징
- 배열의 특징을 그대로 이어받음
- 원소들은 메모리의 연속된 위치에 저장된다
- 빠른 접근 & 수정: 주어진 위치의 원소를 반환하거나 변경하는 동작을 O(1)에 수행 가능
- 크기 조정 가능: 기본 배열과 달리 필요 시 크기를 자동으로 늘리거나 줄일 수 있다. 이 동작은 O(n)
- 느린 삽입 및 삭제: 맨 끝에 요소를 추가하는 것은 O(1)이지만, 중간 요소를 추가하거나 제거할 때는 데이터의 이동이 필요하므로 최악의 경우 O(n)
- 배열의 특징을 그대로 이어받음
동적 배열은 동적으로 미리 할당받은 배열을 사용한다. 여기서 이미 할당받은 메모리의 크기를 배열의 용량(capacity), 그리고 실제 원소의 수를 배열의 크기(size)라고 한다.
동적 배열의 크기가 바뀌어야 할 때는 단순하게 새 베열을 동적으로 할당받은 뒤 기존 원소들을 복사하고, 새 배열을 참조하도록 바꿔치기 한다. 이렇게 더 큰 새 배열을 동적으로 할당받고 새 배열에 기존 배열의 내용을 모두 복사한 다음 바꿔치기를 하는 것을 '재할당'이라고 한다.
재할당은 O(n) 시간이 걸리므로 이를 최소화하기 위해 메모리를 할당받을 때 배열의 크기가 커질 때를 대비해 여유분의 메모리를 미리 할당받아 둔다. 또한, 꽉 찼을 때 더 큰 메모리를 할당받을 때 현재 가진 원소의 개수에 비례해서 여유분을 확보한다. 대표적으로 부족할 때마다 용량을 두 배로 할당하는 방식을 사용한다.
팁: add() 연산을 여러 번 수행할 때 배열의 최종 크기가 얼마인지 미리 짐작할 수 있다면, 동적 배열의 용량을 미리 늘려둠으로써 재할당에 드는 비용을 없앨 수 있다. 대부분의 동적 배열 구현체들은 이와 같은 연산을 지원하는데, 자바의 경우 ArrayList의 ensureCapacity()를 호출하여 달성할 수 있다.
연결 리스트
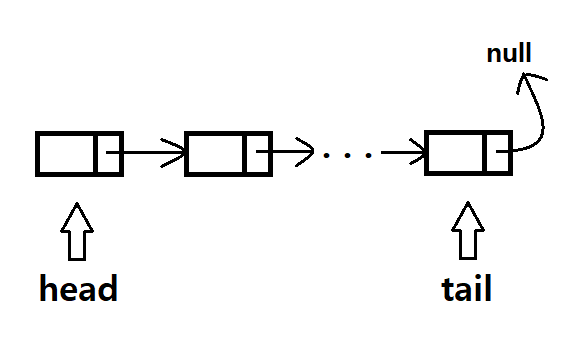
배열 원소들의 순서를 유지하면서 임의의 위치에 원소를 삽입하거나, 임의의 위치에서 원소를 삭제하는 것은 시간이 오래 걸리는 작업이다. 해당 위치 뒤에 있는 원소들으르 하나씩 뒤 혹은 앞으로 옮겨야 하기 때문이다. 이는 보통 O(n) 시간이 소요된다. 이러한 문제를 해결하기 위해 고안된 자료 구조가 연결 리스트(Linked List)이다. 이 역시 대부분의 언어에서 표준 라이브러리에서 제공하며 자바에서는 LinkedList가 있다.
- 특징
- 원소들이 메모리 여기저기 흩어져 있음
- 노드(Node)로 구성: 각 노드는 데이터와 다음 노드의 참조(주소)를 포함.
- 유연한 크기: 크기가 고정되지 않아 삽입/삭제가 빠름. 단순히 참조만 변경해주면 됨. -> O(1)
- 느린 접근: 특정 인덱스에 접근하려면 순차 탐색이 필요 -> O(n)
- 느린 크기 계산: 연결 리스트의 크기를 따로 저장하여 관리하지 않는 이상 크기를 계산하기 위해 탐색이 필요 -> O(n)
- 하지만, 자바에서는 size 필드를 유지하기 때문에 크기 계산을 상수 시간에 지원
- 연결 리스트 응용 연산들
- 잘라 붙이기 연산: 다른 리스트를 특정 리스트에 통째로 삽입하는 것을 O(1)에 달성
- C++에서는 지원하지만, 자바에서는 이를 지원하지 않음. 대신 리스트의 크기를 구하는 연산을 지원
- 삭제했던 원소 돌려놓기
- 잘라 붙이기 연산: 다른 리스트를 특정 리스트에 통째로 삽입하는 것을 O(1)에 달성
연결 리스트의 종류
- 단일 연결 리스트 (Singly Linked List)
- 구성: 각 노드는 데이터와 다음 노드에 대한 참조만을 포함
- 특징:
- 한 방향으로만 탐색 가능
- 삽입과 삭제가 효율적 (특히 양쪽 끝에서)
- 반대로 탐색할 수 없기 때문에 마지막 노드에 접근하려면 전체 노드를 순차적으로 탐색해야 함
- 이중 연결 리스트 (Doubly Linked List)
- 구성: 각 노드는 데이터와 함께 이전 노드와 다음 노드에 대한 참조를 포함
- 특징:
- 양방향 탐색이 가능(뒤로도 탐색할 수 있음)
- 삽입/삭제 시 더 많은 정보를 제공하므로, 중간에서의 삽입과 삭제가 더 효율적
- 노드당 더 많은 메모리 공간이 필요
- 자바의
LinkedList는 이중 연결리스트로 구현되어 있음 -> 큐와 덱으로도 사용 가능
- 원형 연결 리스트 (Circular Linked List)
- 구성: 마지막 노드가 첫 번째 노드를 참조하는 형태의 연결 리스트
- 특징:
- 끝에서 처음으로 순환하므로 반복 작업에 유리
- 단일 연결 리스트와 이중 연결 리스트 두 가지 형태가 존재할 수 있음
- 주로 순환 버퍼나 반복적인 작업에서 사용
- 자바에서는 별도로 지원하지 않기 때문에 따로 구현해야 함. 하지만, 포인터가 리스트의 끝에 도달하면 처음으로 옮겨주는 연산만을 직접 구현하여 원형 리스트를 흉내내는 것도 가능
- 원형 이중 연결 리스트 (Circular Doubly Linked List)
- 구성: 마지막 노드가 첫 번째 노드를 참조하고, 첫 번째 노드 또한 마지막 노드를 참조하는 이중 연결 리스트.
- 특징:
- 양방향 순환이 가능
- 순차적 작업이나 순환 큐에서 많이 사용
추가) 원형 연결 리스트 구현 with 자바
class CircularLinkedList {
private Node head;
private Node tail;
class Node {
int data;
Node next;
Node(int data) {
this.data = data;
}
}
// 리스트에 노드 추가
public void add(int data) {
Node newNode = new Node(data);
if (head == null) {
head = newNode;
tail = newNode;
newNode.next = head; // 첫 번째 노드를 가리키게 함
} else {
tail.next = newNode;
tail = newNode;
tail.next = head; // 원형 연결
}
}
// 리스트 출력
public void printList() {
if (head != null) {
Node current = head;
do {
System.out.print(current.data + " ");
current = current.next;
} while (current != head);
System.out.println();
}
}
}
public class CircularLinkedListExample {
public static void main(String[] args) {
CircularLinkedList cll = new CircularLinkedList();
cll.add(10);
cll.add(20);
cll.add(30);
System.out.print("원형 연결 리스트: ");
cll.printList();
}
}동적 배열 vs. 연결 리스트
| 작업 | 동적 배열 | 연결 리스트 |
| 이전 원소 / 다음 원소 찾기 | O(1) | O(1) |
| 맨 뒤에 원소 추가/삭제하기 | O(1) | O(1) |
| 중간에 원소 추가/삭제하기 | O(n) | O(1) |
| 임의의 위치의 원소 찾기 | O(1) | O(n) |
| 크기 구하기 | O(1) | O(n) 혹은 구현에 따라 O(1) |
- 삽입과 삭제를 할 일이 없거나, 배열의 끝에서만 하면 될 경우 -> '동적 배열' 선택
- 임의의 원소를 접근하는 것이 아니라 모든 원소들을 순회하며 삽입과 삭제를 해야 하는 경우 -> '연결 리스트' 선택
'Data Structure' 카테고리의 다른 글
| [Data Structure] 그래프의 정의와 표현 (2) | 2024.12.08 |
|---|---|
| [Data Structure] 유니온 파인드 (3) | 2024.12.05 |
| [Data Structure] 세그먼트 트리와 이진 인덱스 트리 (2) | 2024.12.04 |
| [Data Structure] 트리, 이진 검색 트리, 우선 순위 큐와 힙 (1) | 2024.12.02 |
| [Data Structure] 큐와 스택, 덱 (1) | 2024.11.27 |

